Generalized Symmetries and Equivalences of Geometric Data
PERIOD: 01.03.2021 – 29.02.2024
funding source:
- GAČR (Grantová Agentura České Republiky)
- 21-08009K – Zobecněné symetrie a ekvivalence geometrických dat
- Slovenian Research and Innovation Agency (ARIS)
- N2-0181 – Posplošene simetrije in ekvivalence v geometrijskih podatkih
partners:
- University of West Bohemia in Pilsen, Czech Republic
- Department of Computer Science and Engineering (UWB-CSE)
- Department of Mathematics (UWB-M)
- University of Maribor, Slovenia
coordinators and contacts:
- Borut Žalik, David Podgorelec (UM FERI)
- Ivana Kolingerová (UWB)
abstract:
An object has symmetry if there is a transformation that maps the object onto itself. Being symmetric is a potentially very useful feature, and symmetries in the natural world have often inspired people when producing tools, buildings, artwork etc. Consequently, symmetry detection became a challenging topic particularly in pattern recognition, computer vision, computer graphics, and geometric modelling, where it addresses problems such as object alignment, data compression, symmetrical editing, reconstruction of incomplete objects, or technical illustrations support.
Three complementary groups of scientists share their know-how in the GeoSym project in order to make progress on hot topics in symmetries:
- the computer graphics group from UWB-CSE, Czech Republic: oriented to development and implementation of geometrical algorithms,
- the mathematicians from UWB-M, Czech Republic: studying the formalized and generalized concepts in geometry and geometrical algorithms, and
- the computer scientists from UM FERI, Slovenia: with expertise in Earth Observation (EO) data processing.
Based on previous research activities of all three teams and identified symmetry-related challenges, the following research objectives have been established:
- O1: Development of fast and reliable methods for detection of generalized symmetries, considering besides the global perfect reflectional symmetry also local, rotational (axial), rigid, weak (approximate) symmetries, for uniform as well as highly non-uniformly distributed or perturbed input point sets and for continuous curves/surfaces.
- O2: Development of new methods for detection and computation of exact projective equivalences for finite sets of points (solutions of polynomial systems) and for further special algebraic varieties (mainly surfaces in 3-space), and of approximate equivalences and symmetries of perturbed objects.
- 03: Improved accuracy of semantic segmentation and object recognition in EO data, achieved by integration of detected symmetries into our existing EO data fusion methodology, and validated in a dedicated set of applications.
We met these objectives by introducing innovative approaches to the detection and quantification of global and local symmetries of geometric shapes in fields ranging from computer graphics to EO data processing. The new methods improve both the quality of the results and the computational efficiency of existing algorithms, having great potential in applications such as shape reconstruction from incomplete data or advanced analysis of structures (shapes and connections) in a wide variety of spatial data use areas such as geosciences, mechanical engineering, civil engineering, medicine, etc. We have evaluated them on four practical examples, including railway line detection, some proof-of-concept steps at incorporating the tree canopies’ symmetries into tree species classification, water level determination in an intermittent lake, and prostate cancer detection.
In total, we announced 9 papers in journals with JCR impact factor and 8 conference publications. We exceeded our forecast by publishing 16 JCR IF papers, 7 conference papers (the lack of one paper has been compensated by several publications in other categories), 1 book chapter, and 2 papers in non-JCR journals, while successfully obtaining a patent from the European Patent Office. The distribution of publications across the project objectives is also adequate.
 |  |
| Satellite image Sentinel-2 of northern Dalmation. | Detected global mirror symmetry. |
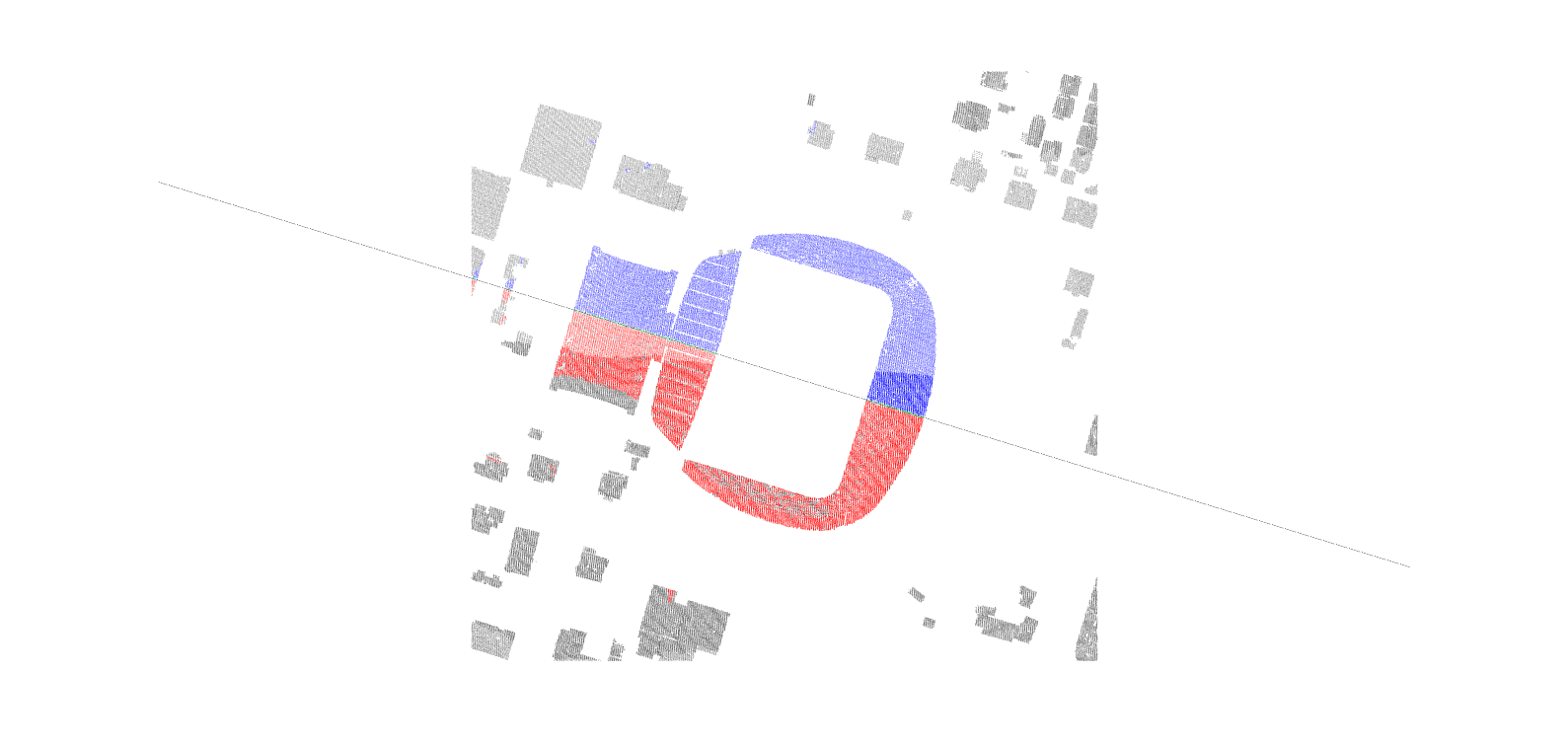 |
| The strongest local reflection symmetry detected over Maribor’s Ljudski vrt stadium and surrounding buildings. |
 |
| Strongest local reflection symmetry detected over buildings and trees in Slomšek Square, Maribor |
    |
| Objects with global reflection symmetry. |
    |
| Objects with multiple global reflection symmetries. |
    |
| Non-symmetric objects with the best found approximate global reflection symmetry. |
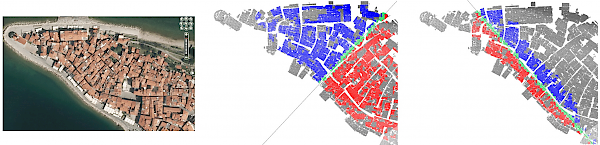 |
| Piran: digital orthophoto (from ARSO LiDAR GIS Viewer), strongest and 14,055th strongest partial reflection symmetries. |
 |
| The Grad castle: digital orthophoto (from ARSO LiDAR GIS Viewer), strongest partial and local reflection symmetries on 1 m voxels. |
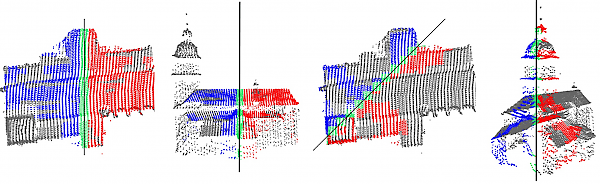 |
| The Maribor Cathedral: strongest and 23rd strongest partial reflection symmetry (both in top and side view). |
This project has received funding from the Slovenian Research and Innovation Agency under the “Public Call for co-financing the Slovenian part of bilateral or tripartite joint research projects CEUS, where GA ČR acts as the Lead Agency”. Research grant N2-0181.




